
Zadanie Inspektor (ins)
Pomóż nam usprawnić bazę zadań!
Inspektor
Limit pamięci: 128 MB
Inspektor Bajtazar bada zbrodnię, która wydarzyła się w biurze informatyków. Próbuje teraz ustalić chronologię zdarzeń. Niestety, informatycy są jednostkami stosunkowo roztrzepanymi. Żaden z nich nie udziela rozsądnych informacji, mówią raczej: "No, kiedy zajrzałem na serwer o 14:42, to zobaczyłem, że zalogowanych w pracy jest pięciu innych informatyków".
Wiadomo, że każdy z informatyków tego dnia przyszedł do biura, spędził w nim trochę czasu i wyszedł. Żaden informatyk nie opuszczał biura pomiędzy swoim przyjściem a wyjściem i nie pojawiał się w biurze poza tym odcinkiem czasu.
Bajtazar nie jest pewien, czy może polegać na zeznaniach informatyków. Chce się dowiedzieć, czy w ogóle możliwe jest, żeby wszyscy mówili prawdę. Poprosił Cię o pomoc.
Wejście
W pierwszym wierszu standardowego wejścia znajduje się liczba całkowita  (
(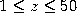 ),
oznaczająca liczbę zestawów danych.
W kolejnych wierszach znajdują się opisy
),
oznaczająca liczbę zestawów danych.
W kolejnych wierszach znajdują się opisy  zestawów danych.
zestawów danych.
W pierwszym wierszu opisu znajdują się dwie liczby całkowite
 i
i 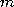 oddzielone pojedynczym odstępem (
oddzielone pojedynczym odstępem (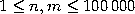 ).
Oznaczają one odpowiednio liczbę informatyków w biurze i liczbę zeznań zebranych przez Bajtazara.
Informatycy są ponumerowani od 1 do
).
Oznaczają one odpowiednio liczbę informatyków w biurze i liczbę zeznań zebranych przez Bajtazara.
Informatycy są ponumerowani od 1 do  .
.
W każdym z kolejnych 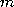 wierszy opisane jest jedno zeznanie.
Każdy z tych wierszy zawiera trzy liczby całkowite
wierszy opisane jest jedno zeznanie.
Każdy z tych wierszy zawiera trzy liczby całkowite 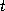 ,
, 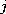 oraz
oraz 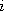 pooddzielane pojedynczymi odstępami
(
pooddzielane pojedynczymi odstępami
(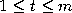 ,
, 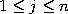 ,
, 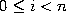 ).
Oznaczają one, że informatyk numer
).
Oznaczają one, że informatyk numer 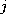 zeznał, iż w chwili
zeznał, iż w chwili 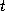 był w biurze i
oprócz niego było tam jeszcze
był w biurze i
oprócz niego było tam jeszcze 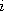 innych informatyków.
Większa liczba oznacza późniejszą chwilę.
Przyjmujemy, że informatycy przychodzili do pracy i wychodzili z pracy w czasie
przed, po lub pomiędzy chwilami, których dotyczą zeznania.
innych informatyków.
Większa liczba oznacza późniejszą chwilę.
Przyjmujemy, że informatycy przychodzili do pracy i wychodzili z pracy w czasie
przed, po lub pomiędzy chwilami, których dotyczą zeznania.
W testach wartych łącznie 7% punktów zachodzi dodatkowy warunek 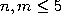 .
Ponadto w testach wartych łącznie 28% punktów zachodzi dodatkowy warunek
.
Ponadto w testach wartych łącznie 28% punktów zachodzi dodatkowy warunek 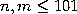 .
.
Wyjście
Dla każdego zestawu danych Twój program powinien wypisać na standardowe wyjście jedną dodatnią liczbę całkowitą.
Wypisanie liczby 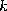 (
(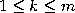 ) oznacza, że pierwsze
) oznacza, że pierwsze 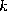 zeznań podanych
na wejściu dla danego zestawu może być prawdziwych,
natomiast pierwsze
zeznań podanych
na wejściu dla danego zestawu może być prawdziwych,
natomiast pierwsze 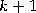 zeznań nie może być prawdziwych.
W szczególności, jeśli
zeznań nie może być prawdziwych.
W szczególności, jeśli 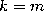 , to wszystkie zeznania podane na wejściu mogą być prawdziwe.
, to wszystkie zeznania podane na wejściu mogą być prawdziwe.
Przykład
Dla danych wejściowych:
2 3 5 1 1 1 1 2 1 2 3 1 4 1 1 4 2 1 3 3 3 3 0 2 2 0 1 1 0
poprawną odpowiedzią jest:
4 3
Wyjaśnienie do przykładu: W pierwszym zestawie danych nie wszystkie zeznania mogą być prawdziwe. Informatycy 1 i 2 zeznali, że byli w biurze przynajmniej od chwili 1 do chwili 4, natomiast informatyk 3 zeznał, że w chwili 2 w biurze była tylko jedna osoba oprócz niego. Jeśli odrzucimy ostatnie zeznanie, to pozostałe mogą już być prawdziwe. Wystarczy, żeby informatyk 2 wyszedł z biura między chwilą 1 i 2.
W drugim zestawie danych wszystkie złożone zeznania mogą być prawdziwe.
Testy "ocen":
- 1ocen:
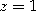 ,
, 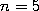
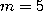 , wszystkie zeznania są ze sobą zgodne,
żaden informatyk nie widział się z żadnym innym;
, wszystkie zeznania są ze sobą zgodne,
żaden informatyk nie widział się z żadnym innym;
- 2ocen:
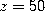 , w każdym zestawie danych
, w każdym zestawie danych 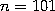 ,
, 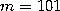 .
W zestawach o nieparzystych indeksach wszystkie zeznania są ze sobą zgodne i każdy informatyk widział się z każdym innym.
Zestawy o parzystych indeksach różnią się tym, że zeznania dotyczące jednego momentu
są składane przez większą liczbę informatyków, niż wynika to z owych zeznań.
.
W zestawach o nieparzystych indeksach wszystkie zeznania są ze sobą zgodne i każdy informatyk widział się z każdym innym.
Zestawy o parzystych indeksach różnią się tym, że zeznania dotyczące jednego momentu
są składane przez większą liczbę informatyków, niż wynika to z owych zeznań.
- 3ocen:
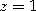 ,
, 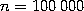 ,
, 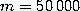 , wszystkie zeznania poza
jednym wyglądają tak samo, zaś to jedno pozostałe jest z nimi sprzeczne.
, wszystkie zeznania poza
jednym wyglądają tak samo, zaś to jedno pozostałe jest z nimi sprzeczne.
Autor zadania: Jakub Wojtaszczyk.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English